设

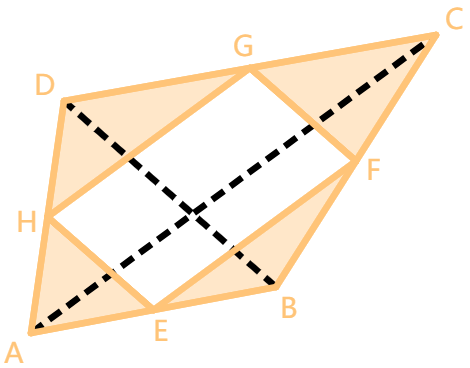
假设四边形是凸的, 如图所示(凹的情况也类似). 添加两条辅助线

首先需要证明:三角形

根据题意,有线段
因此, 三角形
同理, 三角形
因此,
同理,
由此可见,
故内部四边形
从证明中, 我们发现顺次连结四边形各边中点而成的四边形
它被称为瓦里尼翁平行四边形, 面积是原四边形面积的一半.
完成本期挑战需要达到:
初中数学水平
如图,

设

假设四边形是凸的, 如图所示(凹的情况也类似). 添加两条辅助线

首先需要证明:三角形

根据题意,有线段
因此, 三角形
同理, 三角形
因此,
同理,

由此可见,
故内部四边形
从证明中, 我们发现顺次连结四边形各边中点而成的四边形
它被称为瓦里尼翁平行四边形, 面积是原四边形面积的一半.