赶车人

正弦定理

如图, 有一个锐角三角形, 边为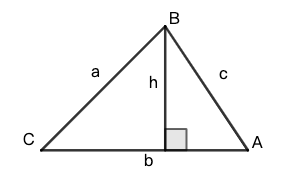, 对应角分别为, 为边上的高. 观察左边的直角三角形有,

同理, 右边的三角形有,

联立得,

即.

同理有, .

将上面的等式串联起来, 就可以得出正弦定理.

文章开头推导正弦定理用的是锐角三角形. 那么正弦定理对直角三角形和钝角三角形也成立吗？

直角三角形中该结论显然成立.

下面我们来说明在钝角三角形中正弦定理仍然成立.

在上图中, 假设角是钝角, 则边上的高

同锐角三角形.

因此正弦定理对钝角三角形同样成立.

拓展的正弦定理

进一步,

这一比值等于多少呢？

在几何中, 我们知道任何三角形都有外接圆, 同一条弦所对的圆周角大小都相同.

如图, 做三角形的外接圆, 并沿圆的周长以角A滑动顶点, 直到三角形的一条边通过圆心. 此时角的大小不会改变.

这就产生了一个包含角的直角三角形, 我们看到等于除以圆的直径.

不妨设边为, 对应角分别为的三角形, 外接圆直径为.

因此有

此即为拓展的正弦定理.

那么你能用正弦定理完成今天的挑战题吗?