吃披萨的时候你有没有想过这样一个问题:如何用最少的切割数切出尽可能多的披萨块? 将这个问题抽象,就有了下面这个数学问题.
例 ( 直线分圆问题 )
如图,

这是高中数学一道经典的直线分圆问题, 常见的作法是根据递推关系求出通项公式. 由于本题研究的是线, 面之间的关系, 欧拉公式
欧拉公式
平面上的欧拉公式是针对平面连通图而言的. 我们先解释一下什么是平面图, 什么是连通图.
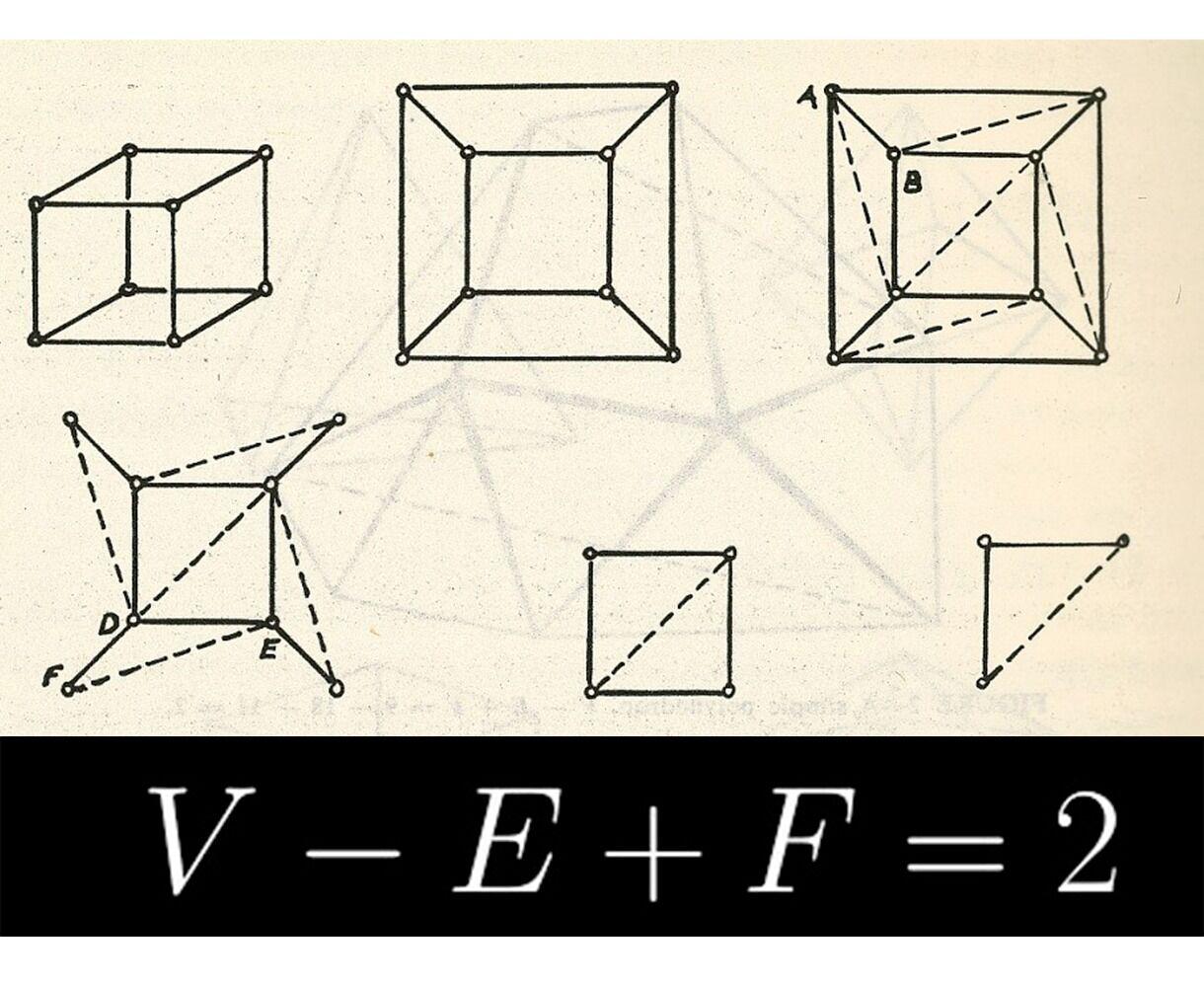
平面图是指可以画在平面上并且不同的边可以互不交叠的图. 其中边是指连接两个顶点的线段. 我们用几个例子来解释这个定义.(举例的图形中顶点均用红色标记.)
比如, 下面这幅图是平面图.

下面这幅

那么下面这幅有

是!因为可以将一条对角线移到外面, 使得边不相交, 如下图所示:

接着介绍连通图. 如果图中任意两点都是连通的, 那么图被称作连通图. 其中两点连通是指存在从一点到另一点的路径.
比如上述3幅图都是连通图.
有了对平面图连通图的理解, 下面就可以给出平面上的欧拉公式.
定理 ( 欧拉公式 )
对于连通的平面图, 顶点数
定理 由法国数学家
 Leonhard Euler
Leonhard Euler was a Swiss mathematician who made enormous contibutions to a wide range of mathematics and physics including analytic geometry, trigonometry, geometry, calculus and number theory.
提出.
Leonhard Euler
Leonhard Euler was a Swiss mathematician who made enormous contibutions to a wide range of mathematics and physics including analytic geometry, trigonometry, geometry, calculus and number theory.
提出.
其中顶点是指图上的点, 边是连接两个顶点的(曲)线段, 面是指被边分成一块块的区域, 并且这里的面不但包含被边围在内部的面, 而且还包含最外面没有边界限制、延伸至无穷远的那个面.
举个例子, 下图是连通的平面图, 满足公式

欧拉公式有很多证明方法, 感兴趣的读者可以查阅文献 [1].
问题分析
回到我们的直线分圆求最大区域数问题, 从特殊情况易得如下结论:
命题 ( 最大化原则 )
有若干条直线分割圆面, 要想分得的区域数最多, 则要求直线两两相交, 交点两两不重合(任意三条直线不共点).
那么接下来我们研究问题都是基于这个原则, 即所作图形都是直线两两相交, 交点两两不重合.
那么最大区域数是否可以用平面上的欧拉公式求解呢?我们先来判断所求问题是否满足欧拉公式的使用条件.
以特殊情况为例, 在圆上作

这显然不是平面图. 那么如果我们将直线间的交点看成是图的顶点, 如下图所示,

啊哈, 这样就符合平面图的定义了, 并且此时顶点之间两两连通, 于是此图为连通的平面图. 而根据图形的构造过程, 结合组合计数原理很容易计算顶点数和边数, 从而利用欧拉公式可以快速求出面数.
特殊情形的分析可以推广到一般的情况, 下面我们就直接对一般问题进行计算.
问题求解
在圆上作
- 顶点数
包含圆周边缘顶点数 和圆内部顶点数, 由于直线两两相交, 交点不重合, 于是圆内部顶点数为 , 所以
- 边数
包含圆周边缘弧线数 和内部直线段数 , 其中内部直线段是这样数的:共有 条直线, 其中每条直线都被其他 条直线分成了 段, 所以共有 .所以
- 欧拉公式中的面数
包含了外层延伸至无穷远的那个面, 而直线分圆面所求区域数 只统计圆内的区域, 不包含那个面, 所以
至此问题得到了解决 [2]. 不得不感叹, 欧拉公式确实是数学上最美公式之一.
更多思考
将本文开头的问题改变一些条件, 我们还可以思考下面这些问题:
若干条直线最多可以将平面分成多少区域?
若干条封闭曲线(比如圆, 椭圆)最多可以将平面分成多少区域?
将二维问题推广到三维, 若干个平面最多可以将空间分成多少部分?推广到更高维度呢?
- Twenty-one Proofs of Euler's Formula. https://www.ics.uci.edu/~eppstein/junkyard/euler/. ⬅
- T. S. Michael.How to Guard an Art Gallery[M].Baltimore: The Johns Hopkins University Press. 2009:1-13. ⬅