当观看皮克斯动画工作室(Pixar)出品的动画电影时, 你是否被里面制作精细的3D人物造型所惊艳到?那些丰富的细节到底是如何制作出来的呢?本文将为你揭示其背后的数学奥秘:计算机图形学(Computer Graphics)中几何建模(Geometric Modeling)的基础——曲线(面)细分(Subdivision).
本文将以高中生也能读懂的方式来讲解曲线细分技术, 其中涉及如何用递推数列及矩阵乘法描述细分的过程, 以及如何用数学方法得到最终的光滑曲线, 希望大家喜欢.
曲线(面)细分——让线条及表面变得更光滑
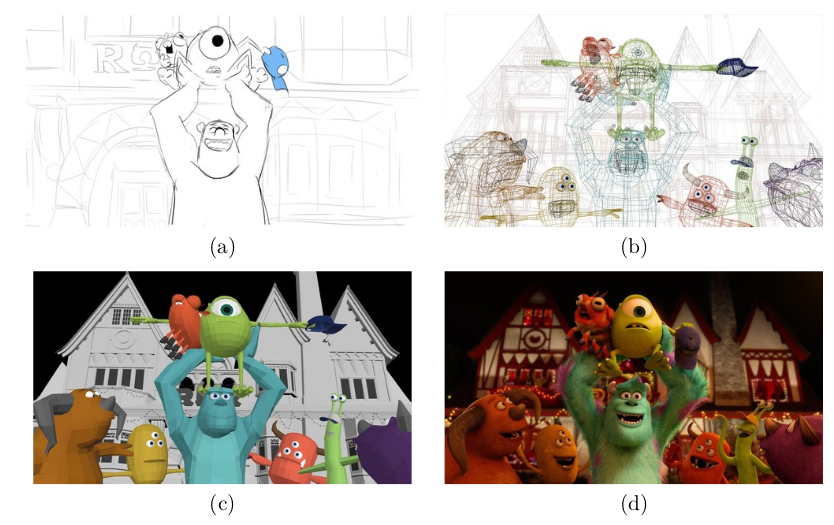
上面四张图展示了《怪兽大学》(Monsters University)中的一个画面场景的制作流程, 从最简单的分镜脚本(a), 到网格状的原型(b)、再到平面着色的预览图(c)、最终得到具有更多纹理和阴影的极具真实感的画面.
要完成一部动画电影的制作, 显然是浩大的工程, 涉及到很多专业技术, 其中就包括我们今天要介绍的曲线(面)细分技术(以下简称细分技术), 这是一种通过不断分割不断调整的方式, 使线条及表面变得更光滑的技术.
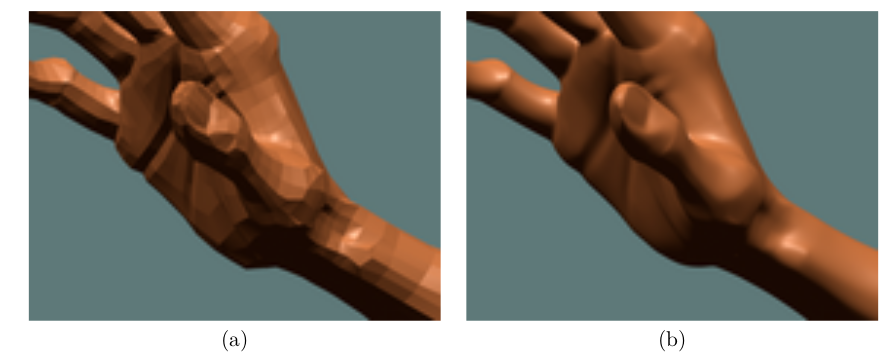
上图是皮克斯在1997年制作的动画短片《棋局》(Geri's Game)中主角的一只手. 实际上, 在当时短片的制作过程中, 是由该片的导演, 恰好也是一位雕塑家, 先雕刻出一个模型扫描进电脑(a), 然后再通过细分技术得到更真实的效果(b).
本文为了简单起见将重点介绍曲线细分, 空间曲面细分所用的原理与思想方法与平面曲线大致是相同, 但是实现起来就要复杂一点.
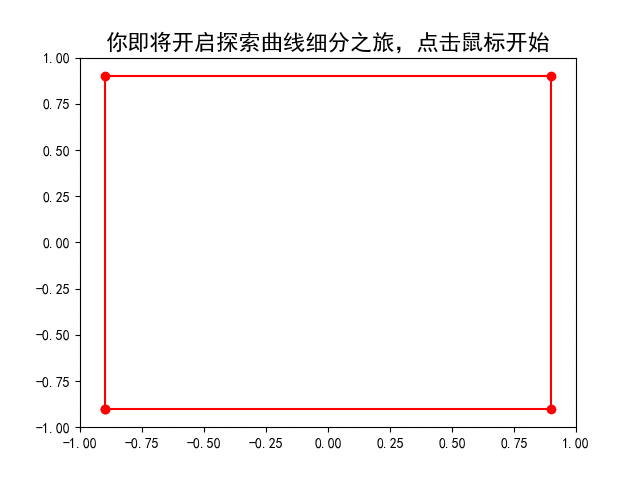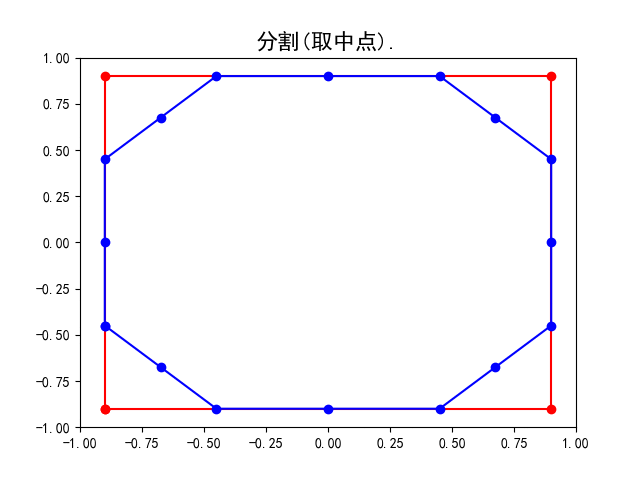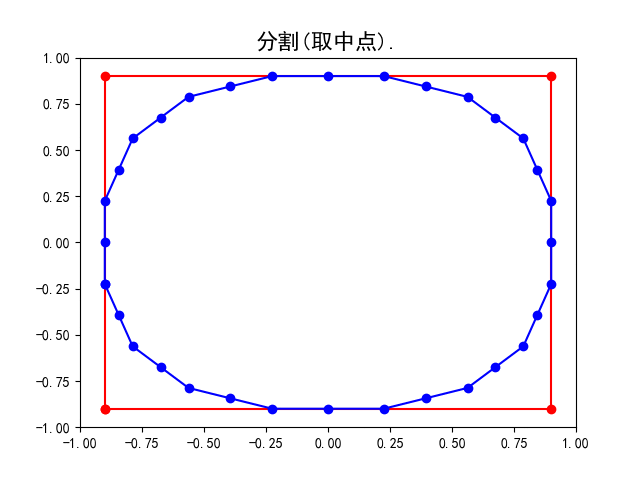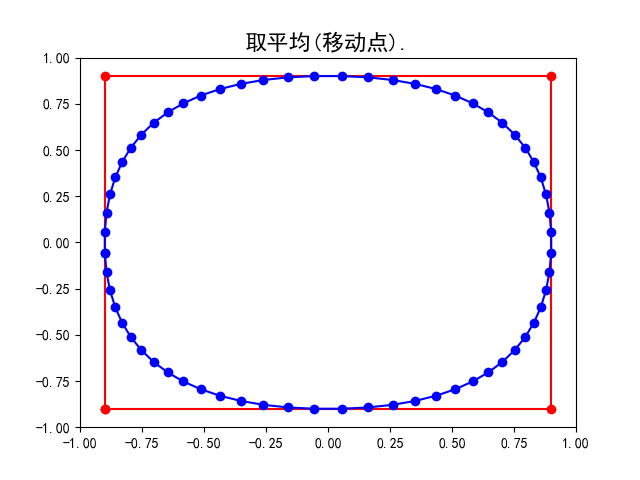
如下图所示, 不难想像一条连接正方形四个顶点的封闭曲线通过细分变为了一条光滑的类似内切圆的封闭曲线(实际上并不是内切圆), 而另一条不太规则的封闭曲线所围成的多边形通过细分变为了一条大致保留原来轮廓的光滑曲线.
下面我们就来揭示上面所采用的细分技术的具体实施步骤(算法).
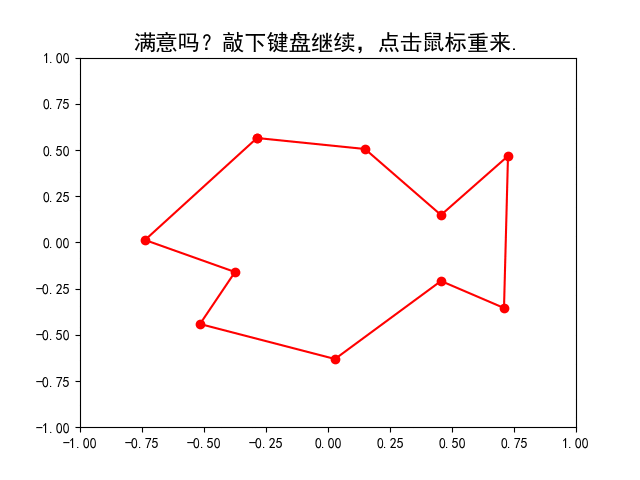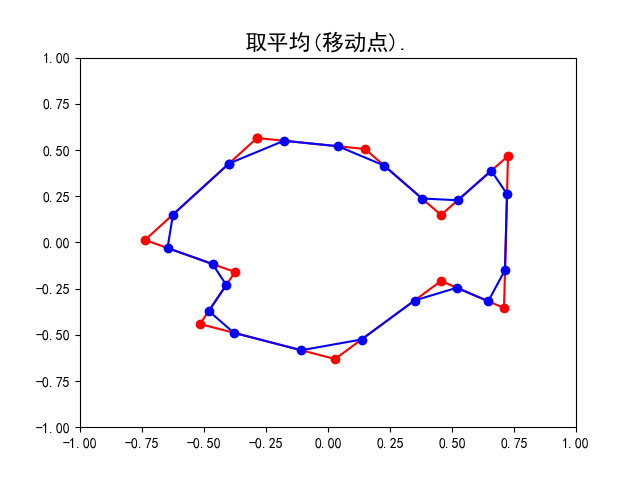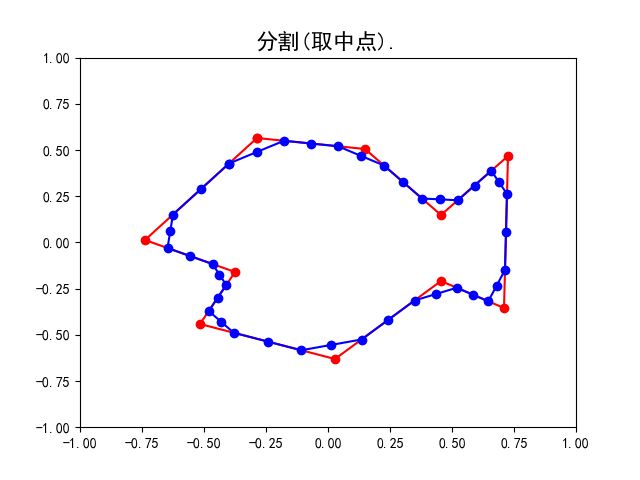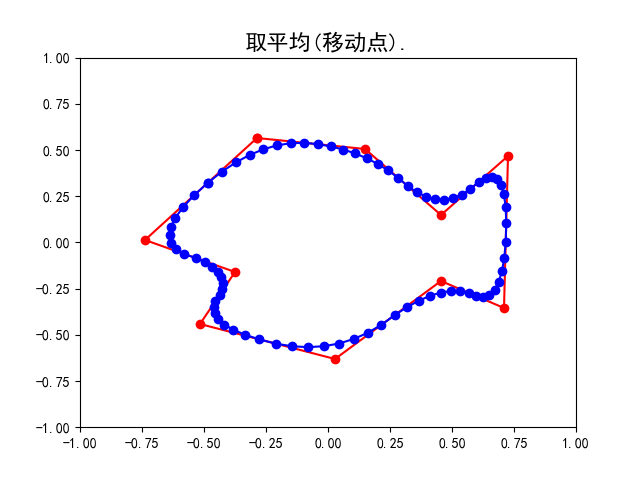
细分:分割与平均
如上面动画所演示的, 首先我们有一些点组成的有序列表(以下简称点列), 并用线段连接相邻两点, 即得到一条初始曲线(为了回避对曲线边界情况的处理, 本文仅讨论封闭曲线的情况, 即认为点列首尾相邻). 然后不断重复下述两个步骤.
- 分割
作出原曲线上各条线段的中点插入到原有的点列,即完成对原曲线的分割. 此时点列中点的个数变为原来的两倍.
- 平均
计算点列中所有相近的一些点的加权平均, 得到新的点列. 比如计算所有相邻两个点的平均即中点, 这些中点即组成新的点列. 然后连结其中所有相邻两点得到调整后的新曲线. 此时点列中点的个数并未发生改变, 只是其中的点发生了改变(移动).
当曲线完成一次分割、平均操作, 也被称为曲线完成了一次细分.
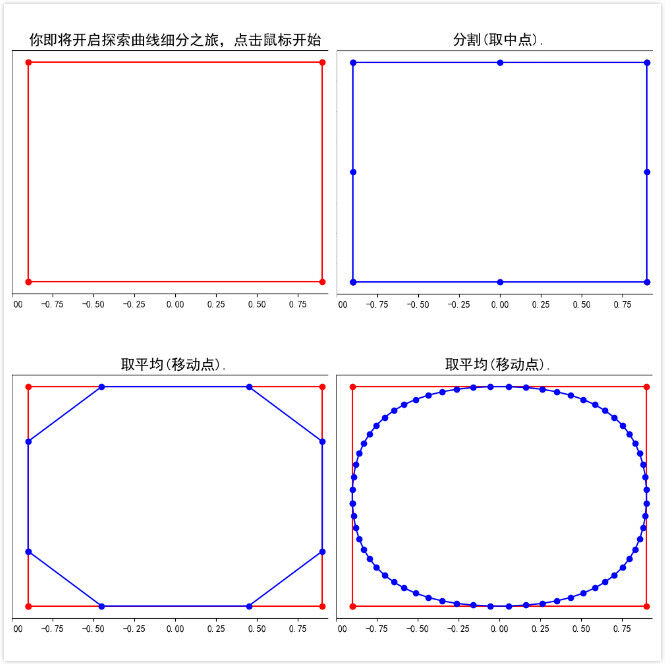
具体地, 请看上面的示意图, 我们用蓝色标记点列中的点. 从上左图到上右图完成了分割, 点列由原来正方形的四个端点变为八个点;从上右图到左下图完成了平均, 点列中的点即上右图中八个点相邻两点的中点. 而右下图是重复多次细分操作后所得的曲线, 不难想象在经过无穷多次操作后即会得到一条光滑曲线(多边形的边长无限趋近于0).
上述平均的操作被称为“1-1法则”, 另外还有“1-2-1法则”, 即调整了参与加权平均操作点的个数及权重, 变为由所有两两相邻的3个点参与权重为1,2,1的加权平均.
下面我们将这个细分过程数学化, 写出每一步操作前后点列之间的递推关系.
细分与递推数列
我们不妨把
为了记号的简洁, 接下来我们使用以下点的加法和数乘运算,
现有点
显然, 点的加法和数乘运算同样满足实数中的运算性质. 故我们可以得到点列
采用1-1法则, 综合两式可得,
一般地, 我们把经过
注意, 当
通过观察
细分与矩阵乘法
为了记号的简洁, 我们把初始点列记作
下面我们列出一些分割操作中点列
故得到
注意, 这里的矩阵并不是方阵, 而是
同理可得, 采取1-1法则, 经过平均操作, 点列
利用矩阵乘法的结合律, 得到
其中
无穷多次细分后的极限
之前我们提到在经过无穷多次细分后, 我们会得到一条光滑曲线. 当我们已知平均的规则后, 其实并不需要利用计算机进行无穷多次递推或矩阵乘法计算来得到光滑曲线, 相反多次计算会造成很大的累计误差。通过对矩阵的特征值分析, 我们得到矩阵
本文不对矩阵的特征值和特征向量展开, 所以会在不影响总体理解的情况下于下文中尽可能回避它们.
按照“1-1法则”的细分
为了控制所研究问题的规模, 我们这里可以仅考虑找到光滑曲线上一点的方法. 而我们已经知道采用“1-1法则”的细分, 每次都是作出原曲线所有线段的两个四等分点, 那么就有这样一个结论:
命题 1 ( “1-1法则”细分定理 )
按照上述“1-1法则”, 曲线上任意一条线段经无穷多次细分后, 该线段的中点落在细分后的极限位置.
不妨设
证明:
由递推关系,
两式相加, 得到
两式相减, 得到
故
由极限的运算性质解得,
得证.
其实我们研究一条线段上两个点的变化即等价于我们研究矩阵
按照“1-2-1法则”的细分
这次我们目标同样是找到极限光滑曲线上的一点. 如图(a)我们来看曲线上一个由相邻三点组成的局部,
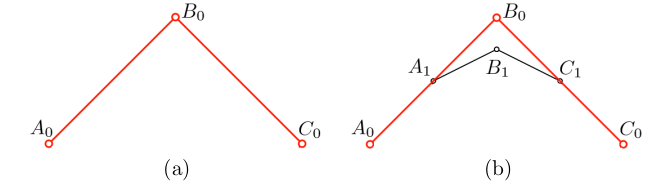
如图, 经过一次分割得到
代换等式右边的
而
此时即得到经过一次细分的曲线上的三点
故得到递推关系如下,
其中
利用特征值分析, 我们可以得到当
由
即得到, 当
即
我们也可以通过递推关系代入计算验证得到,
同理可得,
而由
更多平均法则
实际上除了上述“1-1法则”和“1-2-1法则”两种曲线细分方式还有很多其他选择, 只要稍微调整参与加权平均的点的个数及它们的权重, 就可以得到一种新的细分方式, 但是只有对求加权平均的这一操作进行精心的设计才能获得比较好的效果(比如较好保留原来的轮廓并最终稳定在一条光滑曲线). 比如“1-3-3-1”、“1-4-6-4-1”法则, 即帕斯卡三角上的组合数作为权重的平均操作就被认为效果不错. 但是“1-(-2)-3”就无法稳定在一条光滑曲线上,如下图.
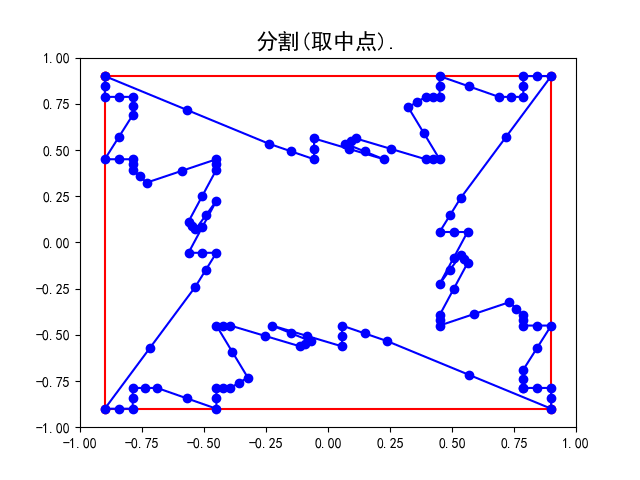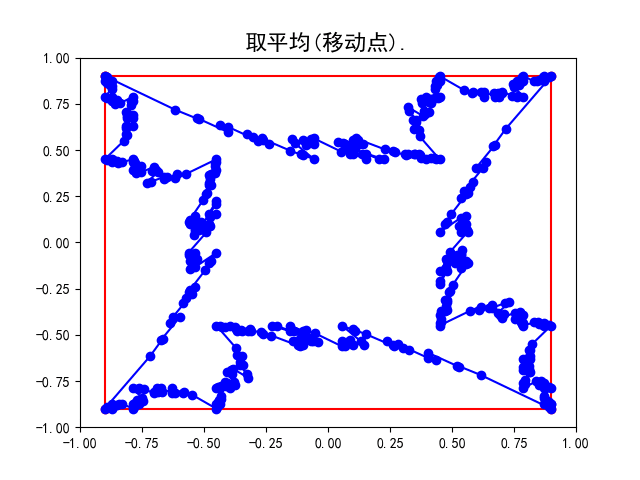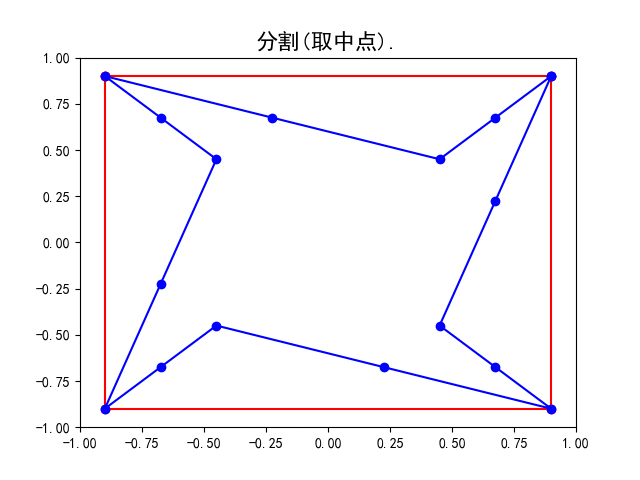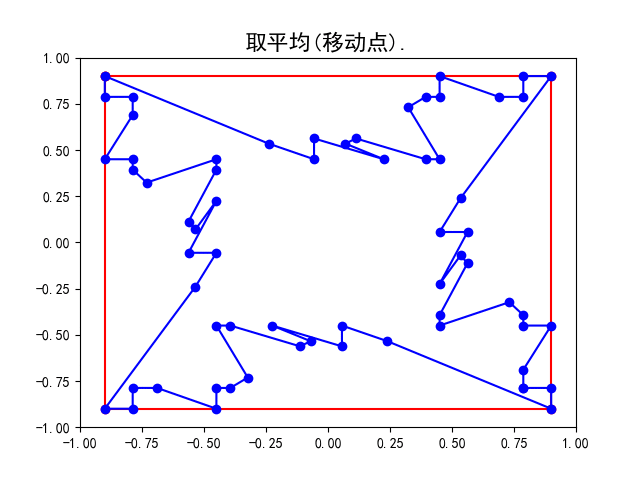
感兴趣的读者可以在Github上的mistc项目主页上获得Python脚本自己动手实验, 也欢迎大牛提交代码完善更多功能.
另外皮克斯工作室发表的论文Subdivision Surfaces in Character Animation中, 包含了对三维曲面细分的简单介绍.
参考文献
[1] David Borland, Tim Chartier and Tabitha Peck.Pixar’s Linear Algebra[J]. Spring 2016: IMAGE 56.
[2] Tony DeRose, Michael Kass, Tien Truong. Subdivision Surfaces in Character Animation.Pixar Animation Studios.
[3] Fletcher Dunn, 3D Math Primer for Graphics and Game Development.
[4] Peter Shirley, Fundamentals of Computer Graphics
本文最早于2019年5月发布于橘子数学公众号. 并有一道配套习题:
现有有序点列
(i) 作出该折线段上所有相邻两点的中点, 此操作称为 " 分割 " ;
(ii) 继续作该折线上所有相邻两点的中点, 并依次连结这些中点得到新的折线段, 此操作称为 " 平均 " ;
(i)、(ii)操作合称为一次 " 细分 " . 原折线段进行一次细分操作后, 就会得到一条新的折线段.
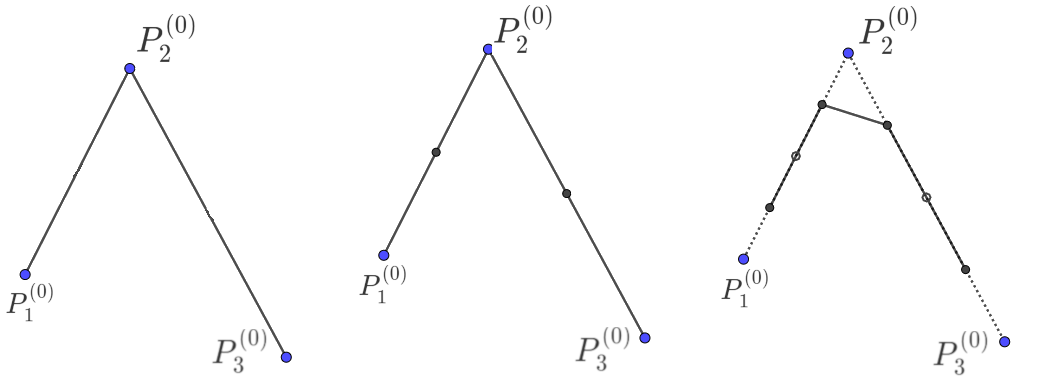 若不断对新得到的折线段重复上述操作, 即可得到一条光滑曲线, 这条曲线被称为Chaikin曲线, 这一过程称为曲线细分.
若不断对新得到的折线段重复上述操作, 即可得到一条光滑曲线, 这条曲线被称为Chaikin曲线, 这一过程称为曲线细分.
- 设折线段
- 在(1)的基础上, 写出
- 若将折线段
